Basic Statistics - Algebra II
Card 0 of 1812
Determine the interquartile range of the following numbers:
42, 51, 62, 47, 38, 50, 54, 43
Determine the interquartile range of the following numbers:
42, 51, 62, 47, 38, 50, 54, 43
How do you find the interquartile range?
We can find the interquartile range or IQR in four simple steps:
- Order the data from least to greatest
- Find the median
- Calculate the median of both the lower and upper half of the data
- The IQR is the difference between the upper and lower medians
Step 1: Order the data
In order to calculate the IQR, we need to begin by ordering the values of the data set from the least to the greatest. Likewise, in order to calculate the median, we need to arrange the numbers in ascending order (i.e. from the least to the greatest).
Let's sort an example data set with an odd number of values into ascending order.


Now, let's perform this task with another example data set that is comprised of an even number of values.

Rearrange into ascending order.

Step 2: Calculate the median
Next, we need to calculate the median. The median is the "center" of the data. If the data set has an odd number of data points, then the mean is the centermost number. On the other hand, if the data set has an even number of values, then we will need to take the arithmetic average of the two centermost values. We will calculate this average by adding the two numbers together and then dividing that number by two.
First, we will find the median of a set with an odd number of values. Cross out values until you find the centermost point

The median of the odd valued data set is four.
Now, let's find the mean of the data set with an even number of values. Cross out values until you find the two centermost points and then calculate the average the two values.

Find the average of the two centermost values.



The median of the even valued set is four.
Step 3: Upper and lower medians
Once we have found the median of the entire set, we can find the medians of the upper and lower portions of the data. If the data set has an odd number of values, we will omit the median or centermost value of the set. Afterwards, we will find the individual medians for the upper and lower portions of the data.

Omit the centermost value.

Find the median of the lower portion.

Calculate the average of the two values.



The median of the lower portion is 
Find the median of the upper portion.

Calculate the average of the two values.



The median of the upper potion is 
If the data set has an even number of values, we will use the two values used to calculate the original median to divide the data set. These values are not omitted and become the largest value of the lower data set and the lowest values of the upper data set, respectively. Afterwards, we will calculate the medians of both the upper and lower portions.

Find the median of the lower portion.

The median of the lower portion is two.
Find the median of the upper portion.

The median of the upper portion is eight.
Step 4: Calculate the difference
Last, we need to calculate the difference of the upper and lower medians by subtracting the lower median from the upper median. This value equals the IQR.
Let's find the IQR of the odd data set.


Finally, we will find the IQR of the even data set.


In order to better illustrate these values, their positions in a box plot have been labeled in the provided image.
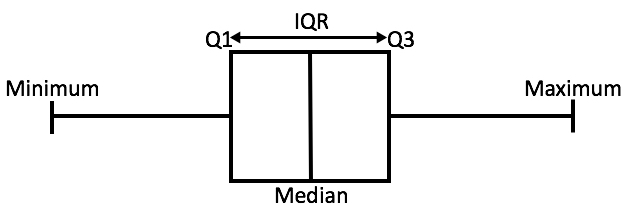
Now that we have solved a few examples, let's use this knowledge to solve the given problem.
Solution:
First reorder the numbers in ascending order:
38, 42, 43, 47, 50, 51, 54, 62
Then divide the numbers into 2 groups, each containing an equal number of values:
(38, 42, 43, 47)(50, 51, 54, 62)
Q1 is the median of the group on the left, and Q3 is the median of the group on the right. Because there is an even number in each group, we'll need to find the average of the 2 middle numbers:


The interquartile range is the difference between Q3 and Q1:

How do you find the interquartile range?
We can find the interquartile range or IQR in four simple steps:
- Order the data from least to greatest
- Find the median
- Calculate the median of both the lower and upper half of the data
- The IQR is the difference between the upper and lower medians
Step 1: Order the data
In order to calculate the IQR, we need to begin by ordering the values of the data set from the least to the greatest. Likewise, in order to calculate the median, we need to arrange the numbers in ascending order (i.e. from the least to the greatest).
Let's sort an example data set with an odd number of values into ascending order.
Now, let's perform this task with another example data set that is comprised of an even number of values.
Rearrange into ascending order.
Step 2: Calculate the median
Next, we need to calculate the median. The median is the "center" of the data. If the data set has an odd number of data points, then the mean is the centermost number. On the other hand, if the data set has an even number of values, then we will need to take the arithmetic average of the two centermost values. We will calculate this average by adding the two numbers together and then dividing that number by two.
First, we will find the median of a set with an odd number of values. Cross out values until you find the centermost point
The median of the odd valued data set is four.
Now, let's find the mean of the data set with an even number of values. Cross out values until you find the two centermost points and then calculate the average the two values.
Find the average of the two centermost values.
The median of the even valued set is four.
Step 3: Upper and lower medians
Once we have found the median of the entire set, we can find the medians of the upper and lower portions of the data. If the data set has an odd number of values, we will omit the median or centermost value of the set. Afterwards, we will find the individual medians for the upper and lower portions of the data.
Omit the centermost value.
Find the median of the lower portion.
Calculate the average of the two values.
The median of the lower portion is
Find the median of the upper portion.
Calculate the average of the two values.
The median of the upper potion is
If the data set has an even number of values, we will use the two values used to calculate the original median to divide the data set. These values are not omitted and become the largest value of the lower data set and the lowest values of the upper data set, respectively. Afterwards, we will calculate the medians of both the upper and lower portions.
Find the median of the lower portion.
The median of the lower portion is two.
Find the median of the upper portion.
The median of the upper portion is eight.
Step 4: Calculate the difference
Last, we need to calculate the difference of the upper and lower medians by subtracting the lower median from the upper median. This value equals the IQR.
Let's find the IQR of the odd data set.
Finally, we will find the IQR of the even data set.
In order to better illustrate these values, their positions in a box plot have been labeled in the provided image.

Now that we have solved a few examples, let's use this knowledge to solve the given problem.
Solution:
First reorder the numbers in ascending order:
38, 42, 43, 47, 50, 51, 54, 62
Then divide the numbers into 2 groups, each containing an equal number of values:
(38, 42, 43, 47)(50, 51, 54, 62)
Q1 is the median of the group on the left, and Q3 is the median of the group on the right. Because there is an even number in each group, we'll need to find the average of the 2 middle numbers:
The interquartile range is the difference between Q3 and Q1:
Compare your answer with the correct one above
Find the median of the set:

Find the median of the set:
The median is the middle number of the set, when it is listed in order from smallest to largest or vice versa. In this case we have an even amount of numbers in the set meaning there are two "middle numbers"- 8 and 13. In order to find the median we take the average of 8 and 13:

The median is the middle number of the set, when it is listed in order from smallest to largest or vice versa. In this case we have an even amount of numbers in the set meaning there are two "middle numbers"- 8 and 13. In order to find the median we take the average of 8 and 13:
Compare your answer with the correct one above
Find the mode of the set:

Find the mode of the set:
The mode is the most repeated number in the set. To answer this, find the number that occurs the most number of times in the set. For this problem that gives us the answer of 11 for the mode.

The mode is the most repeated number in the set. To answer this, find the number that occurs the most number of times in the set. For this problem that gives us the answer of 11 for the mode.
Compare your answer with the correct one above
Find the mean of the set:

Find the mean of the set:
To find the mean, there are two steps:
1. Add all of the numbers in the set together.
2. Divide that number by the amount of numbers are in the set.
For this problem there are 11 numbers in the set, so we add the numbers together and divide by 11 to find the mean:

To find the mean, there are two steps:
1. Add all of the numbers in the set together.
2. Divide that number by the amount of numbers are in the set.
For this problem there are 11 numbers in the set, so we add the numbers together and divide by 11 to find the mean:
Compare your answer with the correct one above
Draw a Box and Whisker plot for the following data set.

Draw a Box and Whisker plot for the following data set.
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.

1st quartile:  ,
,  ,
, 
Median of 1st quartile: 
2nd quartile = Median of total set: 
3rd quartile:  ,
,  ,
, 
Median of 3rd quartile: 
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:

The endpoints (black dots) represent the smallest and largest values, in this case, 2 and 39.
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile: 

Median of 1st quartile:
2nd quartile = Median of total set:
3rd quartile: 

Median of 3rd quartile:
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:

The endpoints (black dots) represent the smallest and largest values, in this case, 2 and 39.
Compare your answer with the correct one above
Draw a Box and Whisker plot for the following data set.

Draw a Box and Whisker plot for the following data set.
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile: 
Median of 1st quartile: 
2nd quartile = Median: 
3rd quartile:
Median of 3rd quartile: 
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:

Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile:
Median of 1st quartile:
2nd quartile = Median:
3rd quartile:
Median of 3rd quartile:
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:

Compare your answer with the correct one above
Draw a box and whisker plot for the following data set.

Draw a box and whisker plot for the following data set.
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile: 
Median of 1st quartile: 
2nd quartile = Median: 
3rd quartile: 
Median of 3rd quartile: 
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:

Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile:
Median of 1st quartile:
2nd quartile = Median:
3rd quartile:
Median of 3rd quartile:
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:

Compare your answer with the correct one above
Draw a Box and Whisker plot for the following data set.

Draw a Box and Whisker plot for the following data set.
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile: 
Median of 1st quartile: 
2nd quartile= Median: 
3rd quartile: 
Median of 3rd quartile: 
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines.
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile:
Median of 1st quartile:
2nd quartile= Median:
3rd quartile:
Median of 3rd quartile:
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines.
Compare your answer with the correct one above
Draw a Box and Whisker plot for the following data set.

Draw a Box and Whisker plot for the following data set.
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile: 
Median of 1st quartile: 
2nd quartile = Median: 
3rd quartile: 
Median of 3rd quartile: 
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile:
Median of 1st quartile:
2nd quartile = Median:
3rd quartile:
Median of 3rd quartile:
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:
Compare your answer with the correct one above
Draw a Box and Whisker plot for the following data set.

Draw a Box and Whisker plot for the following data set.
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile: 
Median of 1st quartile: 
2nd quartile = Median: 
3rd quartile: 
Median of 3rd quartile: 
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:
Put the data in numerical order (from smallest to largest) if it isn't already. In order to find the median, divide the data into two halves. In order to divide the values into quartiles, find the median of the two halves.
1st quartile:
Median of 1st quartile:
2nd quartile = Median:
3rd quartile:
Median of 3rd quartile:
To construct the Box and Whisker Plot we use the minimum and the maximum value in the data set as the ends of the whiskers. To construct the box, we plot a line at the median of the 1st quartile, the median of our total data set, and at the median of the 3rd quartile. Then we connect the tops and bottom of the lines. The result is as follows:
Compare your answer with the correct one above

The box and whisker plot above can be used to find all of the following information about the data set that it describes except:

The box and whisker plot above can be used to find all of the following information about the data set that it describes except:
The median value of the data set, 86, is represented by the dashed line inside the box.
The maximum and minimum of the data set, 100 and 75 (respectively), are found at the far ends of the 2 whiskers on either end.
The range of the data set is found by subtracting the minimum from the maximum; 100-75=25, so the range is 25.
The upper and lower quartiles are given by the two boundaries between the box and the whiskers: the lower quartile (1st quartile) is the left boundary, 80 in the data set; the upper quartile (3rd quartile) is the right boundary, which is 92 in the data set.
All of the other choices are provided by the box and whisker plot, so the correct choice is "The box and whisker plot gives you all of these"
The median value of the data set, 86, is represented by the dashed line inside the box.
The maximum and minimum of the data set, 100 and 75 (respectively), are found at the far ends of the 2 whiskers on either end.
The range of the data set is found by subtracting the minimum from the maximum; 100-75=25, so the range is 25.
The upper and lower quartiles are given by the two boundaries between the box and the whiskers: the lower quartile (1st quartile) is the left boundary, 80 in the data set; the upper quartile (3rd quartile) is the right boundary, which is 92 in the data set.
All of the other choices are provided by the box and whisker plot, so the correct choice is "The box and whisker plot gives you all of these"
Compare your answer with the correct one above
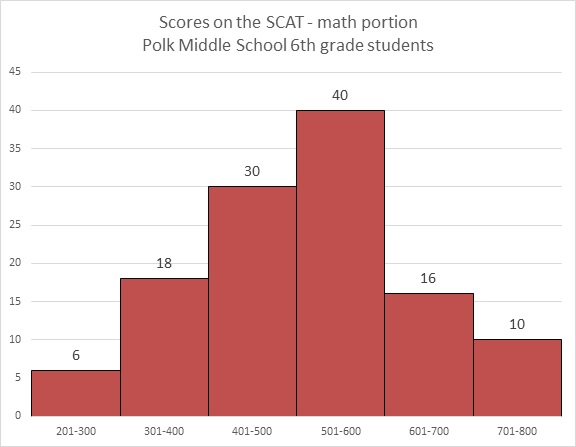
Refer to the above graph. Carla, a sixth grader at Polk, outscored 101 of the students who took the test. Which of these could her score have been?

Refer to the above graph. Carla, a sixth grader at Polk, outscored 101 of the students who took the test. Which of these could her score have been?
 students achieved scores between 200 and 600, and Carla outscored all of them.
students achieved scores between 200 and 600, and Carla outscored all of them.
 students achieved scores between 200 and 700. However, Carla did not outscore all of them.
students achieved scores between 200 and 700. However, Carla did not outscore all of them.
Carla's score had to have been between 600 and 700, so of the five choices, 660 is the only possible one.


Carla's score had to have been between 600 and 700, so of the five choices, 660 is the only possible one.
Compare your answer with the correct one above

Above is a stem-and-leaf representation of the scores on a test administered to a group of students. What was the midrange of the scores?

Above is a stem-and-leaf representation of the scores on a test administered to a group of students. What was the midrange of the scores?
The midrange is the mean of the highest and lowest scores.
Each "stem" in the left column represents the tens digits of the scores; each of the numbers in its row, or "leaf" represents the units digits. The lowest score is represented by the 4 "leaf" in the "3" row - that is, it is 34 - and the highest score is represented by the 8 "leaf" in the "9" row - that is, 98. The midrange is therefore

The midrange is the mean of the highest and lowest scores.
Each "stem" in the left column represents the tens digits of the scores; each of the numbers in its row, or "leaf" represents the units digits. The lowest score is represented by the 4 "leaf" in the "3" row - that is, it is 34 - and the highest score is represented by the 8 "leaf" in the "9" row - that is, 98. The midrange is therefore
Compare your answer with the correct one above

Refer to the above bar graph.
How many students at Polk Middle School scored above 550 on the math portion of the SCAT?

Refer to the above bar graph.
How many students at Polk Middle School scored above 550 on the math portion of the SCAT?
The dividing points of the intervals used to classify students on this graph occur at multiples of 100. No details are given for each interval beyond the number of students who scored in it, so, for example, within the interval 500-600, it is not made clear how many of the 40 students scored above or below 550. The answer is that insufficient information is provided.
The dividing points of the intervals used to classify students on this graph occur at multiples of 100. No details are given for each interval beyond the number of students who scored in it, so, for example, within the interval 500-600, it is not made clear how many of the 40 students scored above or below 550. The answer is that insufficient information is provided.
Compare your answer with the correct one above
The following histogram shows the highest level of education attained by the employees of a local store.
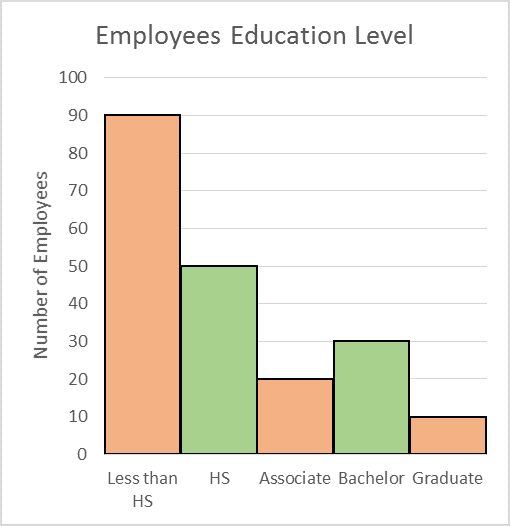
How many employees are working for the store?
The following histogram shows the highest level of education attained by the employees of a local store.

How many employees are working for the store?
Solution
The height of each bar shows the number of employees who attained that particular level of education. So to find the total number of employees, we add the numbers shown by all the bars in the histogram.

The total number of employees is 200.
Solution
The height of each bar shows the number of employees who attained that particular level of education. So to find the total number of employees, we add the numbers shown by all the bars in the histogram.
The total number of employees is 200.
Compare your answer with the correct one above
Find the mean of the set:

Find the mean of the set:
To find the mean, there are two steps:
1. Add all of the numbers in the set together.
2. Divide that number by the amount of numbers are in the set.
For this problem there are 11 numbers in the set, so we add the numbers together and divide by 11 to find the mean:

To find the mean, there are two steps:
1. Add all of the numbers in the set together.
2. Divide that number by the amount of numbers are in the set.
For this problem there are 11 numbers in the set, so we add the numbers together and divide by 11 to find the mean:
Compare your answer with the correct one above
The following histogram shows the highest level of education attained by the employees of a local store.

How many employees have at least an Associate degree?
The following histogram shows the highest level of education attained by the employees of a local store.

How many employees have at least an Associate degree?
Solution
The number of employees who have at least an Associate degree include the employees who have an Associate degree, the employees who have a Bachelor degree and the employees who have a Graduate degree.
We read the numbers from the 3 bars on the histogram showing the employees with Associate, Bachelor, and Graduate degrees.

Solution
The number of employees who have at least an Associate degree include the employees who have an Associate degree, the employees who have a Bachelor degree and the employees who have a Graduate degree.
We read the numbers from the 3 bars on the histogram showing the employees with Associate, Bachelor, and Graduate degrees.
Compare your answer with the correct one above
This histogram shows the distribution of grades on Mr. Margarine's final. What percentage of the students got an A or B?

This histogram shows the distribution of grades on Mr. Margarine's final. What percentage of the students got an A or B?
The histogram shows that there are a total of 23 students.
There were 7 students who earned B's and 5 who earned A's, so that's 12 who got A's or B's.
 , or
, or  .
.
The histogram shows that there are a total of 23 students.
There were 7 students who earned B's and 5 who earned A's, so that's 12 who got A's or B's.


Compare your answer with the correct one above
Which of the following represents a positive association in a scatterplot?
Which of the following represents a positive association in a scatterplot?
A positive association is defined as a scatterplot on which the best fit line has a positive slope.
This pattern is identified because on the graph, looking from left to right, the vast majority of the points goes up.
This can also be described by saying, "as  increases,
increases,  increases".
increases".
A positive association is defined as a scatterplot on which the best fit line has a positive slope.
This pattern is identified because on the graph, looking from left to right, the vast majority of the points goes up.
This can also be described by saying, "as 

Compare your answer with the correct one above
A scatterplot correlates adult males' height vs. shoe size. What does the point  on the scatterplot represent?
on the scatterplot represent?
A scatterplot correlates adult males' height vs. shoe size. What does the point 
When creating a scatterplot, data is collected. This data is formulated into ordered pairs. Each of these ordered pairs, which are later graphed, represent one person's data. Thus, this particular piece of data would represent one man's height of  inches and that same man's shoe size of
inches and that same man's shoe size of  .
.
When creating a scatterplot, data is collected. This data is formulated into ordered pairs. Each of these ordered pairs, which are later graphed, represent one person's data. Thus, this particular piece of data would represent one man's height of 

Compare your answer with the correct one above