Derivatives of Parametric, Polar, and Vector Functions - AP Calculus BC

Card 0 of 140

Question

$ewline {\vec{r}(t)} = (3e^t+t^3,e^{2t}+t,9e^t+e^{2t}) ewline \textnormal{Calculate } \frac{\mathrm{d} }{\mathrm{d} t}{\vec{r}(t)}$

Answer

In general:

If $ewline \ {\vec{r}(t)} = (f(t),g(t),z(t))$ ,

then $ewline \frac{\mathrm{d} }{\mathrm{d} t}{\vec{r}(t)} = (\frac{\mathrm{d} }{\mathrm{d} t}f(t), \frac{\mathrm{d} }{\mathrm{d} t}g(t),\frac{\mathrm{d} }{\mathrm{d} t}z(t))$

Derivative rules that will be needed here:

Taking a derivative on a term, or using the power rule, can be done by doing the following: $\frac{\mathrm{d} }{\mathrm{d} t} t^n = n * t^{n-1}$

When taking derivatives of sums, evaluate with the sum rule which states that the derivative of the sum is the same as the sum of the derivative of each term: $\frac{\mathrm{d} }{\mathrm{d} t}(t^n+10) = \frac{\mathrm{d} }{\mathrm{d} t}t^n + \frac{\mathrm{d} }{\mathrm{d} t}10 = n*t^{n-1}$

Special rule when differentiating an exponential function: $\frac{\mathrm{d} }{\mathrm{d} t} e^{kt} = ke^{kt}$ , where k is a constant.

In this problem, ${\vec{r}(t)} = ((3e^t + t^3),(e^{2t} + t),(9e^t+e^{2t}))$

$\frac{\mathrm{d} }{\mathrm{d} t}(3e^t + t^3)= \frac{\mathrm{d} }{\mathrm{d} t}3e^t + \frac{\mathrm{d} }{\mathrm{d} t}t^3 = 3e^t + 3t^2$

$\frac{\mathrm{d} }{\mathrm{d} t}(e^{2t} + t)= \frac{\mathrm{d} }{\mathrm{d} t}e^{2t}+ \frac{\mathrm{d} }{\mathrm{d} t}t =2e^{2t} + 1$

$\frac{\mathrm{d} }{\mathrm{d} t}(9e^t+e^{2t})= \frac{\mathrm{d} }{\mathrm{d} t}9e^t + \frac{\mathrm{d} }{\mathrm{d} t}e^{2t} = 9e^t + 2e^{2t}$

Put it all together to get $\frac{\mathrm{d} }{\mathrm{d} t}{\vec{r}(t)}$

$\frac{\mathrm{d} }{\mathrm{d} t}{\vec{r}(t)} = (3e^t + 3t^2,2e^{2t} + 1,9e^t + 2e^{2t})$

Compare your answer with the correct one above

Question

Find the derivative of the following set of parametric equations:

Answer

We start by taking the derivative of x and y with respect to t, as both of the equations are only in terms of this variable:

$\frac{dx}{dt}=6t^2+10t-11$

$\frac{dy}{dt}=14t-4$

The problem asks us to find the derivative of the parametric equations, dy/dx, and we can see from the work below that the dt term is cancelled when we divide dy/dt by dx/dt, leaving us with dy/dx:

$\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{dy}{dt}\frac{dt}{dx}=\frac{dy}{dx}$

So now that we know dx/dt and dy/dt, all we must do to find the derivative of our parametric equations is divide dy/dt by dx/dt:

$\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{14t-4}{6t^2+10t-11}=\frac{2(7t-2)}{6t^2+10t-11}$

Compare your answer with the correct one above

Question

Find the derivative of the following polar equation:

$r=3+8sin\theta$

Answer

Our first step in finding the derivative dy/dx of the polar equation is to find the derivative of r with respect to $\theta$ . This gives us:

$\frac{dr}{d\theta}=8cos\theta$

Now that we know dr/d $\theta$ , we can plug this value into the equation for the derivative of an expression in polar form:

$\frac{dy}{dx}=\frac{\frac{dr}{d\theta}sin\theta+rcos\theta }{\frac{dr}{d\theta }cos\theta-rsin\theta }=\frac{8cos\theta sin\theta+(3+8sin\theta )cos\theta}{8cos^2\theta-(3+8sin\theta)sin\theta }$

Simplifying the equation, we get our final answer for the derivative of r:

$\frac{dy}{dx}=\frac{16cos\theta sin\theta +3cos\theta }{8cos^2\theta -3sin\theta -8sin^2\theta }$

Compare your answer with the correct one above

Question

Given that $f: \mathbb{R}^{n}}\rightarrow \mathbb{R}$ . We define its gradient as :

$abla f =\left[\frac{\partial f}{\partial x_{1}} \cdots \frac{\partial f}{\partial x_{n}}\right]$

Let $f: \mathbb{R}^{n}}\rightarrow \mathbb{R}$ be given by:

$f(x_{1},x_{2},\cdots, x_{n}})=\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

What is the gradient of ?

Answer

By definition, to find the gradient vector , we will have to find the gradient components. We know that the gradient components are that partial derivatives.

We know that in our case we have :

$\frac{\partial f}{\partial x_{i}}=\frac{x_{i}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

To see this, fix all other variables and assume that you have only $x_{i}$ as the only variable.

Now we apply the given defintion , i.e,

$abla f =\left[\frac{\partial f}{\partial x_{1}} \cdots \frac{\partial f}{\partial x_{n}}\right]$

with :

$\frac{\partial f}{\partial x_{1}}=\frac{x_{1}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

$\frac{\partial f}{\partial x_{2}}=\frac{x_{2}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

$\frac{\partial f}{\partial x_{3}}=\frac{x_{3}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

$\vdots$

$\frac{\partial f}{\partial x_{n}}=\frac{x_{n}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

this gives us the solution .

Compare your answer with the correct one above

Question

Let $f:\mathbb{R}^{n}\mapsto \mathbb{R}$ .

We define the gradient of as:

$abla f =\left[\frac{\partial f}{\partial x_{1}} \cdots \frac{\partial f}{\partial x_{n}}\right]$

Let $f=sin(x_{1}+2x_{2}+\cdots nx_{n})$ .

Find the vector gradient.

Answer

We note first that :

$\frac{\partial f}{\partial x_{1}}=cos(x_{1}+2x_{2}+\cdots nx_{n})$

Using the Chain Rule where $x_{1}$ is the only variable here.

$\frac{\partial f}{\partial x_{2}}=2 cos(x_{1}+2x_{2}+\cdots nx_{n})$

Using the Chain Rule where $x_{2}$ is the only variable here.

Continuing in this fashion we have:

$\frac{\partial f}{\partial x_{n}}=ncos(x_{1}+2x_{2}+\cdots nx_{n})$

Again using the Chain Rule and assuming that $x_{n}$ is the variable and all the others are constant.

Now applying the given definition of the gradient we have the required result.

$[cos(x_{1}+2x_{2}+\cdots nx_{n}) \quad 2cos(x_{1}+2x_{2}+\cdots nx_{n})\quad \cdots\quad ncos(x_{1}+2x_{2}+\cdots nx_{n})\]$

Compare your answer with the correct one above

Question

What is the derivative of $r=7sin\theta-6$ ?

Answer

In order to find the derivative $\frac{dy}{dx}$ of a polar equation $r=7sin\theta-6$ , we must first find the derivative of with respect to $\theta$ as follows:

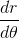$\frac{dr}{d\theta}=7cos\theta$

We can then swap the given values of $\frac{dr}{d\theta}$ and into the equation of the derivative of an expression into polar form:

$\frac{dy}{dx}=\frac{\frac{dr}{d\theta}sin\theta+rcos\theta}{\frac{dr}{d\theta}cos\theta-rsin\theta}$

$\frac{dy}{dx}=\frac{7cos\theta\sin\theta+(7sin\theta-6)\cos\theta}{7cos\theta\cos\theta-(7sin\theta-6)\sin\theta}$

$\frac{dy}{dx}=\frac{7cos\theta\sin\theta+7sin\theta\cos\theta-6\cos\theta}{7cos\theta\cos\theta-7sin\theta\sin\theta+6\sin\theta}$

$\frac{dy}{dx}=\frac{14cos\theta\sin\theta-6\cos\theta}{7(cos^{2}\theta-sin^{2}\theta)+6\sin\theta}$

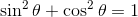Using the trigonometric identity $\sin^{2}\theta+\cos^{2}\theta=1$ , we can deduce that $\cos^{2}\theta=1-\sin^{2}\theta$ . Swapping this into the denominator, we get:

$\frac{dy}{dx}=\frac{14cos\theta\sin\theta-6\cos\theta}{7((1-\sin^{2}\theta)-sin^{2}\theta)+6\sin\theta}$

$\frac{dy}{dx}=\frac{14cos\theta\sin\theta-6\cos\theta}{7(1-2\sin^{2}\theta)+6\sin\theta}$

$\frac{dy}{dx}=\frac{14cos\theta\sin\theta-6\cos\theta}{7-14\sin^{2}\theta+6\sin\theta}$

Compare your answer with the correct one above

Question

Let

$\vec{u}=(\sqrt{1+t^2},2\sqrt{1+t^2},3\sqrt{1+t^2},\cdots n\sqrt{1+t^2})$

What is the derivative of $\vec{u}$ ?

Answer

To find the derivative of this vector, all we need to do is to differentiate each component with respect to t.

Use the Power Rule and the Chain Rule when differentiating.

$(\sqrt{1+t^2})dt=(1+t^2)^\frac{1}{2}dt=\frac{1}{2}(1+t^2)^{-\frac{1}{2}}\cdot 2t=\frac{t}{\sqrt{t^2+1}}$ is the derivative of the first component.

$(2\sqrt{1+t^2})dt=2(1+t^2)^\frac{1}{2}dt=2\frac{1}{2}(1+t^2)^{-\frac{1}{2}}\cdot 2t=\frac{2t}{\sqrt{t^2+1}}$ of the second component.

$\vdots$

$(n\sqrt{1+t^2})dt=n(1+t^2)^\frac{1}{2}dt=n\frac{1}{2}(1+t^2)^{-\frac{1}{2}}\cdot 2t=\frac{nt}{\sqrt{t^2+1}}$ is the derivative of the last component . we obtain then:

$\left(\frac{t}{\sqrt{t^2+1}},\frac{2t}{\sqrt{t^2+1}},\cdots \frac{nt}{\sqrt{t^2+1}}\right)$

Compare your answer with the correct one above

Question

Solve for $\frac{dy}{dx}$ if and .

Answer

We can determine that $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$ since the terms will cancel out in the division process.

Since and , we can use the Power Rule

$\frac{d}{dx}x^{n}=nx^{n-1}$ for all to derive

$\frac{dx}{dt}=(1)2t^{1-1}-(0)5=2$ and $\frac{dy}{dt}=(1)3t^{1-1}+(0)8=3$ .

Thus:

$\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{3}{2}}$ .

Compare your answer with the correct one above

Question

Find the derivative $\frac{dy}{dx}$ of the polar function $r(\theta)=3-4sin(\theta)$ .

Answer

The derivative of a polar function is found using the formula

$\frac{dy}{dx}=\frac{r'(\theta)sin(\theta)+r(\theta)cos(\theta)}{r'(\theta)cos(\theta)-r(\theta)sin(\theta)}$

The only unknown piece is $r'(\theta)$ . Recall that the derivative of a constant is zero, and that

$\frac{d}{d\theta}sin(\theta)=cos(\theta)$ , so

$r'(\theta)=-4cos(\theta)$

Substiting $r'(\theta)\ and\ r(\theta)$ this into the derivative formula, we find

$\frac{dy}{dx}=\frac{-4cos(\theta)sin(\theta)+(3-4sin(\theta))cos(\theta)}{-4cos(\theta)cos(\theta)-(3-4sin(\theta))sin(\theta)}$

$\frac{dy}{dx}=\frac{-4cos(\theta)sin(\theta)+(3-4sin(\theta))cos(\theta)}{-4cos^2(\theta)-(3-4sin(\theta))sin(\theta)}$

Compare your answer with the correct one above

Question

Find the first derivative of the polar function

$r(\theta)=sin(3\theta)$ .

Answer

In general, the dervative of a function in polar coordinates can be written as

$\frac{dy}{dx}=\frac{r'(\theta)sin(\theta)+r(\theta)cos(\theta)}{r'(\theta)cos(\theta)-r(\theta)sin(\theta)}$ .

Therefore, we need to find $r'(\theta)$ , and then substitute $r(\theta)\ and\ r'(\theta)$ into the derivative formula.

To find $r'(\theta)$ , the chain rule,

$\frac{d}{dx}f(g(x))=f'(g(x))g'(x)$ , is necessary.

We also need to know that

$\frac{d}{dx}sin(x)=cos(x)$ .

Therefore,

$r'(\theta)=3cos(3\theta)$ .

Substituting $r(\theta)\ and\ r'(\theta)$ into the derivative formula yields

$\frac{dy}{dx}=\frac{3cos(3\theta)sin(\theta)+sin(3\theta)cos(\theta)}{3cos(3\theta)cos(\theta)-sin(3\theta)sin(\theta)}$

Compare your answer with the correct one above

Question

Given the parametric curve

, $y=\sin{t}$

Evaluate $\frac{dy}{dx}$ when $t = \frac{\pi}{4}$ .

Answer

To find $\frac{dy}{dx}$ , we can use the formula $\frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}}$ .

$\frac{dy}{dt} = \frac{d}{dt}(\sin(t)) = \cos(t)$ .

And $\frac{dx}{dt} = \frac{d}{dt}(2t^2) = 4t$ .

Hence $\frac{dy}{dx} = \frac{\cos(t)}{4t}$ .

Plugging in $t = \frac{\pi}{4}$ , we get

$\frac{\cos(\pi/4)}{4\frac{\pi}{4}} = \frac{\sqrt{2}/2}{\pi} = \frac{\sqrt{2}}{2\pi}.$

Compare your answer with the correct one above

Question

Find $\frac{\mathrm{d} y}{\mathrm{d} x}$ of the following function:

,

Answer

To find the derivative of the parametric function, we must use the following:

$\frac{\mathrm{d} y}{\mathrm{d} x}= \frac{\frac{\mathrm{d} y}{\mathrm{d} t}}{\frac{\mathrm{d} x}{\mathrm{d} t}}$

So, we must take the derivative of each component with respect to t:

$\frac{\mathrm{d} x}{\mathrm{d} t}=2te^t+t^2e^t$

The derivative was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} e^x=e^x$

$\frac{\mathrm{d} y}{\mathrm{d} t}=1$

This derivative was found using the following rule:

$\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

Dividing the two and factoring, we get

$\frac{\mathrm{d} y}{\mathrm{d} t}=\frac{t}{2te^t+t^2e^t}=\frac{t(1)}{te^t(t+2)}=\frac{1}{e^t(t+2)}$

Compare your answer with the correct one above

Question

Find $\frac{\mathrm{d} x}{\mathrm{d} t}$ , where

Answer

To find the derivative of x with respect to t, we must differentiate both sides of the parametric equation with respect to t:

$2x \frac{\mathrm{d} x}{\mathrm{d} t}=3t^2$

The derivatives were found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Note that the chain rule was used when taking the derivative of .

Solving, we get

$\frac{\mathrm{d} x}{\mathrm{d} t}=\frac{3t^2}{2x}$

Compare your answer with the correct one above

Question

A particle moves around the xy plane such that its position as a function of time is given by the parametric function:

$\begin{pmatrix} x(t)\y(t) \end{pmatrix}=\begin{pmatrix} \sin(3t)\\sin(2t) \end{pmatrix}$ .

What is the slope, $\frac{dy}{dx}$ , of the particle's trajectory when $t=\pi/12$ ?

Answer

Evaluate the slope as

$\frac{dy}{dx}=\frac{dy/dt}{dx/dt}$ .

We have

$\frac{dy}{dt}=2\cos(2t)$

and

$\frac{dx}{dt}=3\cos(3t)$

so

$\frac{dy}{dx}=\frac{2\cos(2t)}{3\cos(3t)}$

Evaluating this when $t=\pi/12$ gives

$\frac{dy}{dx}=\frac{2\cos(\frac{\pi}{6})}{3\cos(\frac{\pi}{4})}=\frac{2\left (\frac{\sqrt{3}}{2} \right )}{3\left (\frac{1}{\sqrt{2}} \right )}=\frac{\sqrt{6}}{3}$ .

Remark: This curve is one example from family of curves called Lissajous figures, which can be observed on oscilloscopes.

Compare your answer with the correct one above

Question

Find the derivative of the following set of parametric equations:

Answer

We start by taking the derivative of x and y with respect to t, as both of the equations are only in terms of this variable:

$\frac{dx}{dt}=6t^2+10t-11$

$\frac{dy}{dt}=14t-4$

The problem asks us to find the derivative of the parametric equations, dy/dx, and we can see from the work below that the dt term is cancelled when we divide dy/dt by dx/dt, leaving us with dy/dx:

$\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{dy}{dt}\frac{dt}{dx}=\frac{dy}{dx}$

So now that we know dx/dt and dy/dt, all we must do to find the derivative of our parametric equations is divide dy/dt by dx/dt:

$\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{14t-4}{6t^2+10t-11}=\frac{2(7t-2)}{6t^2+10t-11}$

Compare your answer with the correct one above

Question

Find the derivative of the following polar equation:

$r=3+8sin\theta$

Answer

Our first step in finding the derivative dy/dx of the polar equation is to find the derivative of r with respect to $\theta$ . This gives us:

$\frac{dr}{d\theta}=8cos\theta$

Now that we know dr/d $\theta$ , we can plug this value into the equation for the derivative of an expression in polar form:

$\frac{dy}{dx}=\frac{\frac{dr}{d\theta}sin\theta+rcos\theta }{\frac{dr}{d\theta }cos\theta-rsin\theta }=\frac{8cos\theta sin\theta+(3+8sin\theta )cos\theta}{8cos^2\theta-(3+8sin\theta)sin\theta }$

Simplifying the equation, we get our final answer for the derivative of r:

$\frac{dy}{dx}=\frac{16cos\theta sin\theta +3cos\theta }{8cos^2\theta -3sin\theta -8sin^2\theta }$

Compare your answer with the correct one above

Question

Given that $f: \mathbb{R}^{n}}\rightarrow \mathbb{R}$ . We define its gradient as :

$abla f =\left[\frac{\partial f}{\partial x_{1}} \cdots \frac{\partial f}{\partial x_{n}}\right]$

Let $f: \mathbb{R}^{n}}\rightarrow \mathbb{R}$ be given by:

$f(x_{1},x_{2},\cdots, x_{n}})=\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

What is the gradient of ?

Answer

By definition, to find the gradient vector , we will have to find the gradient components. We know that the gradient components are that partial derivatives.

We know that in our case we have :

$\frac{\partial f}{\partial x_{i}}=\frac{x_{i}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

To see this, fix all other variables and assume that you have only $x_{i}$ as the only variable.

Now we apply the given defintion , i.e,

$abla f =\left[\frac{\partial f}{\partial x_{1}} \cdots \frac{\partial f}{\partial x_{n}}\right]$

with :

$\frac{\partial f}{\partial x_{1}}=\frac{x_{1}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

$\frac{\partial f}{\partial x_{2}}=\frac{x_{2}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

$\frac{\partial f}{\partial x_{3}}=\frac{x_{3}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

$\vdots$

$\frac{\partial f}{\partial x_{n}}=\frac{x_{n}}{\sqrt{{x_{1}^2}+x_{2}^2+\cdots+x_{n}^2}}$

this gives us the solution .

Compare your answer with the correct one above

Question

Let $f:\mathbb{R}^{n}\mapsto \mathbb{R}$ .

We define the gradient of as:

$abla f =\left[\frac{\partial f}{\partial x_{1}} \cdots \frac{\partial f}{\partial x_{n}}\right]$

Let $f=sin(x_{1}+2x_{2}+\cdots nx_{n})$ .

Find the vector gradient.

Answer

We note first that :

$\frac{\partial f}{\partial x_{1}}=cos(x_{1}+2x_{2}+\cdots nx_{n})$

Using the Chain Rule where $x_{1}$ is the only variable here.

$\frac{\partial f}{\partial x_{2}}=2 cos(x_{1}+2x_{2}+\cdots nx_{n})$

Using the Chain Rule where $x_{2}$ is the only variable here.

Continuing in this fashion we have:

$\frac{\partial f}{\partial x_{n}}=ncos(x_{1}+2x_{2}+\cdots nx_{n})$

Again using the Chain Rule and assuming that $x_{n}$ is the variable and all the others are constant.

Now applying the given definition of the gradient we have the required result.

$[cos(x_{1}+2x_{2}+\cdots nx_{n}) \quad 2cos(x_{1}+2x_{2}+\cdots nx_{n})\quad \cdots\quad ncos(x_{1}+2x_{2}+\cdots nx_{n})\]$

Compare your answer with the correct one above

Question

Let

$\vec{u}=(\sqrt{1+t^2},2\sqrt{1+t^2},3\sqrt{1+t^2},\cdots n\sqrt{1+t^2})$

What is the derivative of $\vec{u}$ ?

Answer

To find the derivative of this vector, all we need to do is to differentiate each component with respect to t.

Use the Power Rule and the Chain Rule when differentiating.

$(\sqrt{1+t^2})dt=(1+t^2)^\frac{1}{2}dt=\frac{1}{2}(1+t^2)^{-\frac{1}{2}}\cdot 2t=\frac{t}{\sqrt{t^2+1}}$ is the derivative of the first component.

$(2\sqrt{1+t^2})dt=2(1+t^2)^\frac{1}{2}dt=2\frac{1}{2}(1+t^2)^{-\frac{1}{2}}\cdot 2t=\frac{2t}{\sqrt{t^2+1}}$ of the second component.

$\vdots$

$(n\sqrt{1+t^2})dt=n(1+t^2)^\frac{1}{2}dt=n\frac{1}{2}(1+t^2)^{-\frac{1}{2}}\cdot 2t=\frac{nt}{\sqrt{t^2+1}}$ is the derivative of the last component . we obtain then:

$\left(\frac{t}{\sqrt{t^2+1}},\frac{2t}{\sqrt{t^2+1}},\cdots \frac{nt}{\sqrt{t^2+1}}\right)$

Compare your answer with the correct one above

Question

Solve for $\frac{dy}{dx}$ if and .

Answer

We can determine that $\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$ since the terms will cancel out in the division process.

Since and , we can use the Power Rule

$\frac{d}{dx}x^{n}=nx^{n-1}$ for all to derive

$\frac{dx}{dt}=(1)2t^{1-1}-(0)5=2$ and $\frac{dy}{dt}=(1)3t^{1-1}+(0)8=3$ .

Thus:

$\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{3}{2}}$ .

Compare your answer with the correct one above

Tap the card to reveal the answer