Lagrange Error Bound for Taylor Polynomials - AP Calculus BC
Card 0 of 10
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 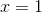 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 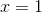
Compare your answer with the correct one above
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 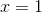 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 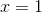
Compare your answer with the correct one above
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 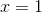 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 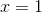
Compare your answer with the correct one above
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 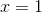 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 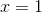
Compare your answer with the correct one above
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 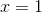 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 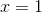
Compare your answer with the correct one above
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 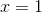 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 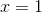
Compare your answer with the correct one above
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 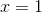 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 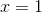
Compare your answer with the correct one above
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 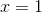 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 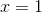
Compare your answer with the correct one above
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 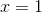 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 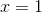
Compare your answer with the correct one above
Let  be the fifth-degree Taylor polynomial approximation for
be the fifth-degree Taylor polynomial approximation for  , centered at
, centered at  .
.
What is the Lagrange error of the polynomial approximation to  ?
?
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating  centered at
centered at  is:
is:

The Lagrange error is the absolute value of the next term in the sequence, which is equal to  .
.
We need only evaluate this at 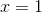 and thus we obtain
and thus we obtain 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to 
We need only evaluate this at 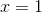
Compare your answer with the correct one above