Modeling by Solving Separable Differential Equations - AP Calculus BC
Card 0 of 10
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
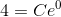

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
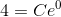

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
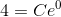

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
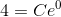

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
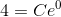

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
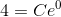

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
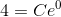

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
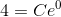

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
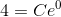

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above
Solve the separable differential equation

with the condition  .
.
Solve the separable differential equation
with the condition 
To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:

Integrating both sides, we get

The rules of integration used were
 ,
, 
The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:

To solve for C, we use our given condition:
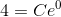

Our final answer is

To solve the separable differential equation, we must separate x and y, dx and dy respectively to opposite sides:
Integrating both sides, we get
The rules of integration used were

The constants of integration merged into one.
Now, we exponentiate both sides of the equation to solve for y, and use the properties of exponents to simplify:
To solve for C, we use our given condition:
Our final answer is
Compare your answer with the correct one above