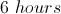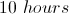Equations
Help Questions
Math › Equations
An art show wants to focus on sculpture but will also accept paintings and drawings. The show has room for 



Explanation
Since the paintings and the drawings have the same ratio, they will have the same number on display.
Let 
Then, 
Set up a proportion:
Solve by cross multiplying to get 

Then add 

Then divide by 

So there are 


Solve the system of equations.
None of the other answers are correct.
Explanation
Isolate 
Plug 

Plug 

Now we have both the 


Solve the system of equations.
None of the other answers are correct.
Explanation
Isolate 
Plug 

Plug 

Now we have both the 


Tom is painting a fence 




If Huck completes painting the entire fence after Tom leaves, how many more hours will Huck work than Tom?
Explanation
Tom paints for a total of 



to determine the total length of the fence Tom paints.

Subtracting this from the total length of the fence 




If Huck works 


Solve the equation for 
No solution
Explanation
Since we have variables on both sides, we first subtract 
This leaves us with 
Subtracting 2 from both sides, we get 
Solve the equation for 
No solution
Explanation
Since we have variables on both sides, we first subtract 
This leaves us with 
Subtracting 2 from both sides, we get 
An art show wants to focus on sculpture but will also accept paintings and drawings. The show has room for 



Explanation
Since the paintings and the drawings have the same ratio, they will have the same number on display.
Let 
Then, 
Set up a proportion:
Solve by cross multiplying to get 

Then add 

Then divide by 

So there are 


Tom is painting a fence 




If Huck completes painting the entire fence after Tom leaves, how many more hours will Huck work than Tom?
Explanation
Tom paints for a total of 



to determine the total length of the fence Tom paints.

Subtracting this from the total length of the fence 




If Huck works 


Solve the pair of equations for x and y:
Explanation
Equation 1:
Equation 2:
Solve equation 2 for X:
Substitute into Equation 1:
Solve for y: 
Take the answer for y and plug it back into either original equation to find x:
Solve:
Explanation
Add the two equations together to get 


Now substitute this 

Next subtract 

Now divide both sides by 

Therefore the answer is