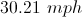Polynomial Functions
Help Questions
Math › Polynomial Functions
List the transformations that have been enacted upon the following equation:
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical compression by a factor of 4
horizontal stretch by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units left
vertical stretch by a factor of 4
horizontal stretch by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 1/4
horizontal compression by a factor of 1/6
vertical translation 7 units down
horizontal translation 3 units right
Explanation
Since the equation given in the question is based off of the parent function 

- If
is greater than 1, the function has been vertically stretched (expanded) by a factor of
.
- If
is between 0 and 1, the function has been vertically compressed by a factor of
.
In this case, 

- If
is greater than 1, the function has been horizontally compressed by a factor of
.
- If
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
.
In this case, 

- If
is positive, the function was translated
units right.
- If
is negative, the function was translated
units left.
In this case, 

- If
is positive, the function was translated
units up.
- If
is negative, the function was translated
units down.
In this case, 
List the transformations that have been enacted upon the following equation:
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical compression by a factor of 4
horizontal stretch by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units left
vertical stretch by a factor of 4
horizontal stretch by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 1/4
horizontal compression by a factor of 1/6
vertical translation 7 units down
horizontal translation 3 units right
Explanation
Since the equation given in the question is based off of the parent function 

- If
is greater than 1, the function has been vertically stretched (expanded) by a factor of
.
- If
is between 0 and 1, the function has been vertically compressed by a factor of
.
In this case, 

- If
is greater than 1, the function has been horizontally compressed by a factor of
.
- If
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
.
In this case, 

- If
is positive, the function was translated
units right.
- If
is negative, the function was translated
units left.
In this case, 

- If
is positive, the function was translated
units up.
- If
is negative, the function was translated
units down.
In this case, 
Let 


Explanation
Substitute 


Let 


Explanation
Substitute 


Solve the following system of equations:
Infinite solutions.
Explanation
We will solve this system of equations by Elimination. Multiply both sides of the first equation by 2, to get:
Then add this new equation, to the second original equation, to get:
or
Plugging this value of 
or
Solve the following system of equations:
Infinite solutions.
Explanation
We will solve this system of equations by Elimination. Multiply both sides of the first equation by 2, to get:
Then add this new equation, to the second original equation, to get:
or
Plugging this value of 
or
It took Jack 25 minutes to travel 14 miles, what was Jack's average speed in mph?
Explanation
* We have to change the time from minutes to hours, there are 60 minutes in one hour.
It took Jack 25 minutes to travel 14 miles, what was Jack's average speed in mph?
Explanation
* We have to change the time from minutes to hours, there are 60 minutes in one hour.
![f(x)=4[6(x-3)]^{4}-7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106187/gif.latex)
![g(x) = a[b(x-c)^{4}]+d](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106188/gif.latex)