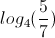Simplifying Logarithms
Help Questions
Math › Simplifying Logarithms
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Solve for
Explanation
Use the power reducing theorem:

Solve for
Explanation
Use the power reducing theorem:

Which of the following expressions is equivalent to 
Explanation
According to the rule for exponents of logarithms,

Which of the following expressions is equivalent to 
Explanation
According to the rule for exponents of logarithms,

Which of the following represents a simplified form of 
Explanation
The rule for the addition of logarithms is as follows:

As an application of this,
Which of the following represents a simplified form of 
Explanation
The rule for the addition of logarithms is as follows:

As an application of this,
Simplify 
Explanation
Using properties of logs we get:
Simplify 
Explanation
Using properties of logs we get: